Chiffrement par cheminement d'une fourmi de Langton
Récemment, j’ai réalisé qu’une fourmi de Langton se promenant sur une image noir et blanc et la modifiant à la volée était un phénomène parfaitement réversible : en programmant une fourmi duale ayant des mécaniques inversées par rapport à la fourmi initiale, on peut en théorie reconstruire le film en sens inverse et retrouver in fine l’image originale. Chiche ? Chiche !
- La fourmi de Langton
- Image de départ
- Algorithme de destruction
- Dégradation de l’image par la fourmi
- Emergence de boucles d’inversion
- Quantification de la perturbation
- Procédure de reconstruction
- Programme de chiffrement (non.)
- Considérations sur la sécurité de l’algorithme
- Pour aller un peu plus loin
La fourmi de Langton
La fourmi de Langton est un petit automate cellulaire que j’aime beaucoup. Les règles, dans leur formulation originelle, sont très simples. La fourmi se déplace sur une grille bi-dimensionnelle dont les cases ne peuvent prendre que deux couleurs : noir ou blanc. La grille est historiquement blanche mais on peut envisager n’importe quel motif de départ (un damier d’échec, une image binarisée, du bruit etc.).
La fourmi est représentée par sa position, que nous notons $(x,y)$ et son orientation (haut, bas, gauche, droite).
Ses règles d’évolution sont les suivantes (l’ordre d’application est important) :
- si elle est sur une case noire, elle fait un quart de tour vers la gauche; sinon (i.e. si elle est sur une case blanche) elle fait un quart de tour vers la droite
- elle change la couleur de la case sur laquelle elle se trouve
- elle avance d’une case
Voici un exemple d’évolution de la fourmi sur une grille $11 \times 11$ et pour les 200 premiers pas, tiré de Wikipédia :

La grille est supposée être infinie ce qui n’est pas réalisable en pratique. D’ordinaire, on peut choisir une grille suffisamment grande pour que la fourmi n’ait pas le temps d’atteindre les bords lors de sa pérégrination qui sera d’un temps fini. Mais on peut également définir des règles sur ce qu’il se passe lorsque la fourmi dépasse les limites de la grille. Habituellement, on considère un comportement à la pacman : si la fourmi sort à droite, elle réapparaît à gauche. Idem pour tous les autres bords (si elle sort en haut, elle réapparaît en bas etc.). C’est ce comportement là que nous envisagerons dans le cas du traitement de nos images (puisqu’idéalement, on aimerait que la fourmi se promène vraiment partout sur notre image et pas seulement “loin des bords”).
Une conjecture étonnante a été émise sur le comportement de la fourmi : au bout d’un certain temps, cette dernière partira à l’infini dans un schéma périodique appelé l’autoroute. Un exemple d’une telle autoroute est donnée ci-dessous (la fourmi y est représentée par un pixel rouge). C’est un comportement émergent, structuré, qui apparaît après une phase de mouvement en apparence chaotique (à tout le moins, irrégulière) de la fourmi. Cet attracteur apparaît systématiquement pour l’ensemble des damiers finis étudiés jusqu’à présent par la communauté scientifique.
Néanmoins, ce n’est pas le sujet de mon article. Je me concentre surtout sur la façon dont la fourmi désagrège, méthodiquement et sans perte d’information une image de départ.
La transformation est à chaque pas totalement réversible puisqu’il suffit d’effectuer les étapes en sens inverser (reculer d’une case, changer la couleur, tourner). A noter que cette caractéristique de réversibilité n’est pas propre à tous les automates cellulaires ainsi que l’illustre cet exemple du jeu de la vie tiré de l’hommage rendu par XKCD lors du décès de John Conway, l’inventeur du jeu. Dans cette configuration, le petit bonhomme se transforme en glyder, une structure qui se déplace à l’infini par translation. On devine bien qu’une fois le glyder établi, il sera impossible de reformer le bonhomme en passant le film en sens inverse : de l’information a été perdue à un moment du processus.

Image de départ
Mais revenons en au propos principal de mon article. Pour les besoins de l’expérience, je me suis basé sur une photo de moi prise à la webcam de mon ordinateur. Je vous prie de bien vouloir excuser le caractère quelque peu narcissique de cette initiative… Je me suis aussi limité à une image de 501 pixels de large par 501 pixels de haut, pour des raisons que nous discuterons bientôt.

C’est, comme vous pouvez le conster, une photo en couleur. Il faut donc la convertir en Noir et Blanc de façon purement binaire (soit Noir, soit Blanc, pas de nuances de gris).
Ma première idée a été de partir sur une fonction de seuillage classique. En choisissant le bon seuil (ici $76$) on garde une bonne compréhension de l’image.
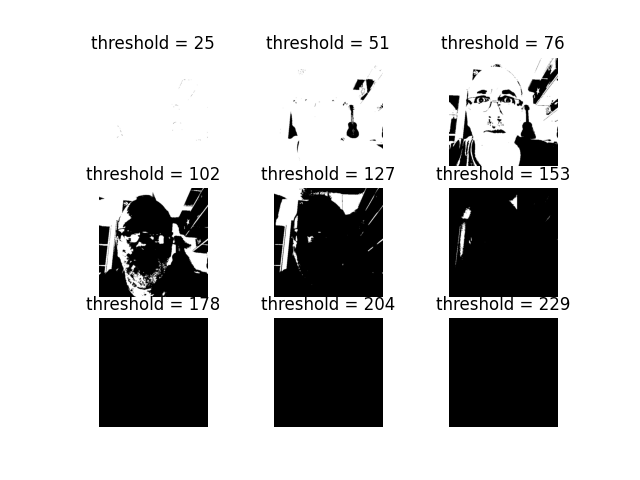
Néanmoins, je trouve qu’on perd quand même pas mal d’information. Je suis alors parti sur une méthode de diffusion d’erreur (le dithering), par un algorithme de Floyd-Steinberg. L’idée est de rendre compte des nuances de gris en utilisant des techniques de propagation d’erreur. Un exemple récent de dithering dans l’univers du jeu vidéo est le réputé Return of the Obra Dinn.
Voici ce qu’on obtient si on applique l’algorithme sur mon image initiale.
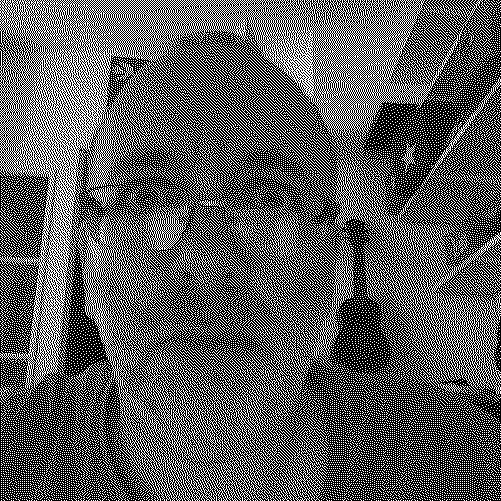
Comprenons bien que l’image obtenue n’est constituée que de pixels soit Noir, soit Blanc; ainsi qu’on peut s’en rendre compte en regardant un zoom sur mon oeil droit.

Outre le fait qu’on a l’impression de perdre moins d’informations sur l’image, ce procédé créé un damier de départ assez complexe qui perturbera le cheminement de la fourmi.
Algorithme de destruction
L’algorithme est assez simple et se base sur la bibliothèque Pillow qui permet de manipuler (trop) simplement des images.
Paramètres globaux
Je commence par définir quelques constantes de l’automate :
WIDTH = 501
HEIGHT = 501
N = int(5*10**6) # Iteration of the Langton's ant
DIR = ['L', 'U', 'R', 'D'] # Ordered directions (Left, Up, Right, Down)
COLORS = ['B', 'W'] # Black or White
dither = [Image.Dither.NONE, Image.Dither.FLOYDSTEINBERG] # I should try which one is cooler
x = (WIDTH-1)//2
y = (HEIGHT-1)//2
d = 1
L’image est, comme nous l’avons dit, de taille constante : WIDTH = 501 pixels de large et HEIGHT = 501 pixels de haut. J’ai choisi une taille d’image assez grande pour qu’on puisse voir quelque chose mais pas trop afin de ne pas attendre trop longtemps que la fourmi ait marché un peu partout. Le choix d’un nombre impair permet de placer la fourmi exactement au centre de l’image. C’est un choix purement esthétique, la position de départ de la fourmi important au final assez peu.
On définit également le nombre N d’itérations maximum (ici 5 millions de pas) afin d’arrêter le processus.
Les variables DIR et COLORS contiennent respectivement les 4 orientations de la fourmi (gauche, haut, droite, bas) et la couleur des cases de l’image (noir ou blanc donc). Les orientations sont stockées de telle façon que l’évolution de la fourmi ne la fait se déplacer que d’une case vers l’avant ou vers l’arrière dans le vecteur d’état : étant intialement orientée “DROITE”, la fourmi ne peut ainsi passer que dans l’état “HAUT” (quart de tour vers la gauche) ou “BAS” (quart de tour vers la droite). J’aurai aimé coder ça sous la forme d’une liste circulaire. Je sais par exemple que la bibliothèque itertools dispose d’une fonction cycle qui permet de faire ce genre de chose. Mais j’ai été un peu fainéant et j’ai rajouté un gros modulo…
La liste dither contient les deux seuls algorithmes actuellement implémentés avec Pillow (version 11.2.1) permettant de réduire la palette chromatique d’une image : le seuillage simple (accessible avec Image.Dither.NONE) et l’algorithme de Floyd-Steinberg dont nous avons déjà parlé et qui s’applique avec Image.Dither.FLOYDSTEINBERG. Hélas, les fonctions proposées par Pillow sont souvent trop basique et il n’est pas possible de définir un paramètre de seuillage. J’ignore comment ce paramètre est choisi (peut-être un simple $255/2$). Mais en pratique, j’ai du me passer de cette fonction de Pillow pour le faire à la main.
L’état initial de la fourmi est finalement représenté par ses coordonnées x = (WIDTH-1)//2 et y = (HEIGHT-1)//2 et son orientation intiale, vers le haut, d = 1. C’est un choix qui est ici purement arbitraire. Remarquons au passage qu’avec Pillow, l’origine du repère est situé au bord supérieur gauche de l’image, comme c’est souvent le cas avec les autres bibliothèques de traitement d’image.
Préparation de l’image
Voici les quelques fonctions clefs qui m’ont permis de préparer mon image avant traitement. Je ne les détaille pas plus et je l’indique uniquement pour en garder une trace.
#%% Loading the picture
img = Image.open('./input.jpg')
#%% Pre-processing of the picture
(w, h) = img.size
s = min(img.size)
box = ((w-s)/2, (h-s)/2, (w-s)/2+s, (h-s)/2+s)
img = img.crop(box) # Crop to a square format
img.thumbnail((WIDTH, HEIGHT), Image.Resampling.BICUBIC) # Interpolation to a 501x501 picture
# Dithered picture
img_dithered = img.convert('1', dither=dither[1])
# Thresholded picture (with a custom threshold parameter)
img_thresholded = img.convert('L')
img_thresholded = img_thresholded.point(lambda p: p > 76 and 255)
img_thresholded = img_thresholded.convert('1', dither=dither[0])
Marche de la fourmi
Voici le coeur du programme, qui code l’évolution de la fourmi pas à pas. Il faut bien entendu encapsuler tout ça dans une boucle sur le nombre de pas (donc jusqu’à N qui vaut cinq millions). Ce n’est pas forcément très bien optimisé. Encore un fois, les listes circulaires pour éviter le recours systématique aux modulo (à la fois sur la direction et sur les pixels de l’image) pourrait améliorer un peu les choses. Mais je ne crois pas qu’on puisse drastiquement réduire le temps de calcul, la fourmi de Langton n’étant par définition pas parallélisable.
c = img.getpixel((x,y))//255
if c==0 : # Black case
d = (d-1)%4
else :
d = (d+1)%4
img.putpixel((x,y), ((c+1)%2) * 255)
match d : # (0,0) coin en haut à gauche !
case 0 :
x -= 1
case 1 :
y -= 1
case 2 :
x += 1
case 3 :
y += 1
if (x >= WIDTH) : x = 0
if (x<0) : x = WIDTH-1
if (y >= HEIGHT) : y = 0
if (y<0) : y = HEIGHT-1
Dégradation de l’image par la fourmi
Voici ce qu’on obtient lorsqu’on fait se promener la fourmi en partant du centre et que nous la laissons évoluer sur cinq millions de pas.
On voit que la fourmi finit bien par passer partout. Je ne sais pas si c’était attendu compte tenu de l’univers clôt et périodique de notre image, mais peut-être la fourmi aurait-elle pu partir à l’infini et rester cloisonnée dans une partie de l’image (par exemple, en allant uniquement de gauche à droite sur une petite bande en hauteur). Ce n’est ici heureusement pas le cas et on arrive cahin-caha à barbouiller l’intégralité de l’image jusqu’à obtenir une littérale bouillie de pixels.
Néanmoins, qu’est-ce que c’est lent ! Avec une image de $501 \times 501$ pixels, une fourmi bien disciplinée qui lirait les pixels ligne après ligne en allant de la gauche vers la droite aurait mis environ 250 000 mouvement pour parcourir l’image. Ici, il nous faut un nombre de mouvements de l’ordre du million, c’est à dire quatre fois plus. Compte tenu du mouvement en apparence erratique de la fourmi, ce n’est pas énormément plus, mais ça reste néanmoins très fastidieux.
On remarque également que, sur la durée de la simulation, la fourmi ne semble jamais être partie en autoroute. Son chemin a toujours été entravé par des pixels qui ont localement perturbé son évolution.
En revanche, il y a quelques chose de plus troublant qui m’a interpelé.
Emergence de boucles d’inversion
A plusieurs reprises, particulièrement au début de la vidéo, la fourmi repasse sur ses pas et rétablit l’image originelle. Je ne m’attendais pas du tout à ce comportement, que je décide d’appeler des boucles d’inversion faute d’un meilleur terme.
En voici un exemple ci-dessous, qui survient très grossièrement entre l’étape $1 \times 10^5$ et $2 \times 10^5$. La fourmi avait commencé à perturber mon crâne et mes joues (à gauche, étape 105 545). A un moment, elle a changé d’avis et a bien tout remis en place (au milieu, étape 177 760). Puis elle est parti barbouiller mes yeux (à droite, étape 205 535).

Elle reconstruit ainsi localement (en espace) et temporairement ce qu’elle a déconstruit avant de reprendre sa marche destructrice.
Elle ne repasse bien évidemment pas exactement sur ses pas (car sinon, elle reviendrait exactement au point de départ), mais pendant un certain nombre d’itérations ses actions font localement ressortir de l’information. Je me demande si cela n’est pas du aux motifs localement périodique introduits par l’algorithme de ditherisation et dont on peut voir un exemple dans le bord inférieur droit de mes lunettes, entouré en rouge ci-dessous.

Creuser un peu plus cette question m’aménerait trop loin mais j’ai néanmoins voulu tester ce que donnerait la marche de la fourmi sur une image seuillée plutot que dithérisée. J’ai donc refait tourner l’algorithme sur une telle image en ayant choisi le seuil de 76 que nous avions considéré en début d’article. En-deça d’une nuance de gris de $76/255$, le pixel devient Noir et Blanc sinon.
Un oeil attentif remarquera toujours quelques boucles, moins elles sont moins nombreuses et surtout beaucoup plus courtes (en temps et en espace). Il y a peut-être quelque chose à creuser dans le fait qu’une fourmi placée au voisinage du passage d’une autre fourmi est susceptible de reconstruire l’image originelle. Sans doute des blocs de transformations équivalent, quelque chose comme ça.
En revanche, les grands aplats uniformes introduits par le seuillage rendent beaucoup plus fréquentes l’émergence d’autoroutes.
Enfin, on remarque que la fourmi peine beaucoup plus à brouiller l’image, le processus semble sensiblement plus lent.
Quantification de la perturbation
Nous pouvons introduire deux mesures de la perturbation causée par la fourmi au fil de sa marche : l’écart quadratique moyen (EQM) par rapport à l’image initiale et l’entropie.
C’est ce qui est tracé ci-dessous pour l’image dithérisée (en bleu) et seuillée (en orange) avec l’EQM en haut et l’entropie en bas.
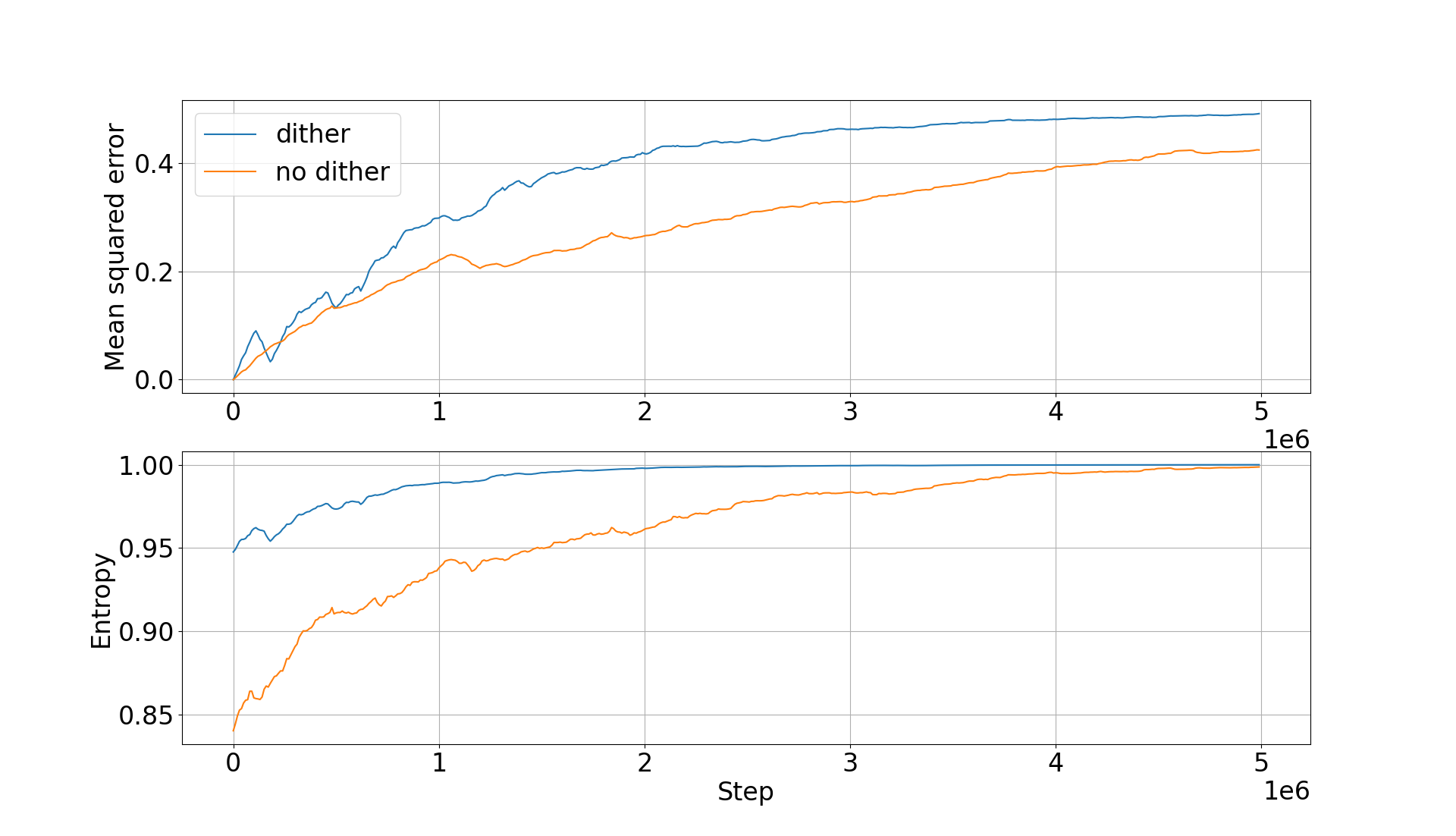
Plusieurs observations notables :
- L’EQM part bien évidemment de zéro au tout début : la fourmi n’introduit initialement aucune modification
- On le voit à la fois sur l’EQM et sur l’entropie : l’image dithérisée se brouille plus rapidement que l’image simplement seuillée. Nous nous en étions rendu compte en comparant les deux vidéos.
- On observe bien les boucles d’inversion lorsque, tout à coup, l’EQM par rapport à l’image initiale chute avant de reprendre. On constate bien de nouveau que l’amplitude de cet effet est plus important pour l’image dithérisée. Gardons en tête que ces courbes sont fortement décimées (un point tous les 10 000 pas). De fait, on est susceptible de ne pas capturer les micro boucles d’inversion qui s’étalent sur moins de 10 000 pas.
- L’entropie initiale est plus élevée pour l’image dithérisée que pour l’image seuillée. La encore c’est attendu puisque dans le cas de l’image seuillée on a tendance à avoir de grands aplats de couleur. L’image est en quelque sorte beaucoup plus ordonnée, beaucoup plus structurée. Alors qu’il s’agit à l’origine de la même image source !
Bien entendu, pour l’EQM il faut garder en tête que ce n’est qu’un indicateur. Un EQM maximal n’est pas forcément souhaitable en ce sens où on obtiendrait une image solarisée de l’image initiale… donc parfaitement lisible !
Procédure de reconstruction
Pour la reconstruction, on pourrait coder le comportement inverse de la fourmi et la faire aller à reculons. Néanmoins, il y a légéremment plus malin : il suffit de lui faire faire un virage à 180° et à lui laisser continuer sa marche. Elle reviendra ainsi sur ses pas et reconstruira méthodiquement tout ce qu’elle avait préalablement détruit.
Ainsi, la fourmi inverse consiste simplement à écrire à un moment :
d = (d+2) % 4
Voici le genre de résultat que nous obtenons alors, en partant de l’image dithérisée, en la brouillant pendant un milliard d’étapes (oui oui), en retournant la fourmi et en la laissant évoluer à nouveau pendant un milliard d’étape (on s’accroche petite fourmi !) :

J’ai trouvé ça très cool à regarder : la fourmi semble se promener de façon chaotique au milieu d’une bouillie de pixels et tout à coup un détail de l’image émerge ! Il grandit petit à petit. Puis la fourmi part faire autre chose… et d’autres détails arrivent, etc.
Programme de chiffrement (non.)
Bon, idéalement j’aurais aimé faire un petit code autonome qui chiffrerait/déchiffrerait une image donnée.
Je me suis alors posé plusieurs questions :
- comment connaître le nombre minimal de pas à partir duquel l’image est bien brouillée ? Une étude dynamique de l’évolution de l’entropie et de l’EQM ? Une boucle qui ne s’arréterait que lorsqu’un seuil à définir aurait été atteint ? (avec un garde fou sur le nombre maximum d’itération quoi qu’il arrive ?)
- comment estimer la montée en charge de l’algorithme ? Doit-on gérer tous les cas de figure de taille d’image ? Que faire si l’utilisateur branche l’algo sur une image 4K (pauvre fourmi !) ?
- si l’utilisateur fournit une image couleur ou en nuances de gris, que fait-on ? Le paramètre de seuillage étudié ici a été estimé visuellement, doit-on coder cela ?
- l’algorithme est-il sensé gérer différents types d’image ? Il est évident que le format de l’image de sortie DOIT ETRE conservateur (adieu le jpg, on n’écrit qu’en png)
- idéalement, il faudrait coder ça en travaillant sur
argvpour récupérer les différents paramètres - mettre ça dans un paquet qui se piloterait soit directement, soit en import python
- en sortie de l’algorithme de chiffrement, il faudrait indiquer les paramètres permettant de déchiffrer l’image obtenue : position et orientation de la fourmi en fin de parcours ainsi que le nombre d’itérations à faire en sens inverse
Je pensais avoir la motivation de le faire mais je sens que je me dégonfle un peu. C’est précisément ce que je n’aime pas trop en informatique : parfois le decorum prend une place démesurée par rapport au coeur du code. Le diable est toujours, toujours, dans les détails.
Considérations sur la sécurité de l’algorithme
Mais in fine, je ne suis pas sûr que cet algorithme soit d’une quelconque utilité. Pour les raisons suivantes.
Déjà il est très lent. Nous l’avons déjà dit et il est inutile de s’attarder plus sur ce fait.
Ensuite, le nombre d’itérations nécessaires pour avoir un brouillage efficace n’est pas connu a priori et peut varier selon les images (comparons pour s’en assurer les performances obtenues avec les images dithérisée et seuillée). Ce n’est pas rédhibitoire en soit mais il faudrait s’interroger sur les performances en moyenne (et en moyenne sur quelle population d’images ?). Il pourrait s’avérer que l’algorithme ne soit pas simplement lent, il pourrait devenir très lent dans la plupart des cas. Notre image dithérisée possède des caractéristiques très particulières qui pourraient optimiser le parcours de la fourmi…
Par ailleurs j’ignore s’il existe des cas où la fourmi ne passe pas par tous les pixels, quel que soit le nombre d’itérations.
On pourrait attendre a minima que la fourmi soit passée au moins une fois par toutes les cases avant d’envisager de s’arrêter. A supposer que cet état puisse seulement être atteint (cf. ma remarque précédente), et en notant $N_0$ ce nombre d’étapes, on pourrait envisager de laisser tourner l’algorithme pendant, mettons, $2\times N_0$ pour s’assurer qu’on mélange vraiment bien toute l’image. Mais ne se pourrait-il pas que, ce faisant, nous arrêtions le processus en plein milieu d’une boucle d’inversion et que l’image, pourtnat longuement chiffrée, laisse transparaître des informations critiques ?
Finalement, le chiffrement n’est pas fort : quiconque dispose de la clef (le triplet $(x,y,d)$ à partir duquel faire cheminer notre fourmi inverse), quiconque dispose de cette clef donc, peut totalement reconstruire l’image. La sécurité de l’image brouillée réside notamment dans la sécurité entourant la clef !
Par ailleurs, si on souhaite décrypter une telle image chiffrée par force brute, il faut considérer ici $501 \times 501 \times 4$ clefs possibles pour la fourmi, soit un million de possibilités. Ajoutons à cela que nous ignorons le nombre d’étapes à attendre avant d’avoir une image lisible. Peut-être, sur ce point là précisément, est-on pas trop mal finalement ? Mais le nombre précis d’itération n’est pas super important, on peut accepter d’avoir une petite trace de fourmi résiduelle…
Pour aller un peu plus loin
Je me doute bien que je n’ai rien découvert de nouveau concernant la fourmi de Langton. Mais j’ai été bien content d’expérimenter un peu quelques trucs cool avec cet automate.
Je sais que la fourmi de Langton appartient à une catégorie assez large de machines de Turing appelées les turmites. En gros, si j’ai bien compris, les turmites sont des machines de Turing particulières qui évoluent sur un plan bi-dimensionnel (notre image) et qui sont caractérisées notamment par leur orientation. Je me demande trois choses.
La première : peut-on “accélérer” un peu le brouillage de l’image en plaçant un nombre arbitraire de fourmis ? Attention c’est casse-gueule car les fourmis risquent de se marcher sur les pieds (littéralement). Il faut bien garder l’ordre du déplacement des différentes fourmis.
La deuxième : nous avons travaillé ici sur des images en Noir et Blanc (soit Noir, soit Blanc) ce qui est le cadre de travail canonique de la fourmi de Langton. Mais peut-on généraliser le processus à des images en niveaux de gris (déjà) et en couleur (ensuite) ?
La troisième : j’ai évoqué en fin d’article l’impossibilité de choisir le jpeg comme format de sortie d’image. Mais j’aimerais bien savoir ce que ça donnerait de volontairement abîmer l’image avant de faire fonctionner la fourmi en sens inverse. Trouverait-on tout de même des bouts d’images reconnaissables ou bien n’obtiendrions-nous qu’une bouillie de pixels (les perturbations du jpeg, localisées au niveau des forts gradients de l’image, ayant en quelque sorte contaminé toute l’image) ?