Un jeu de l'oie coloré
Avec ma fille Alice, nous aimons bien jouer au jeu de l’oie. Nous avons à la maison un coffret de jeux de société pour enfant de la marque Oxybul qui possède une particularité intéressante. En effet, enfin de permettre aux plus petits de jouer, l’un des dés à six faces présente des faces colorées en lieu et place des motifs à base de point.

La mécanique est intéressante et je me suis interrogé sur l’équivalence avec le jeu de l’oie classique.
Présentation du jeu de l’oie simplifié
Le plateau de jeu va de la case départ à la case d’arrivée en 36 cases avec trois échelles ci et là qui permettent d’avancer ou reculer plus rapidement si on s’arrête à leur niveau.
Les cases alternent les couleurs Rouge, Jaune, Bleu et Vert. Le motif périodique contient donc ces quatres couleurs et on remarque que le nombre total de cases est bien un multiple de 4.
Observons maintenant le dé. Je ne résiste pas au plaisir d’en faire un rapide patron sous TikZ.
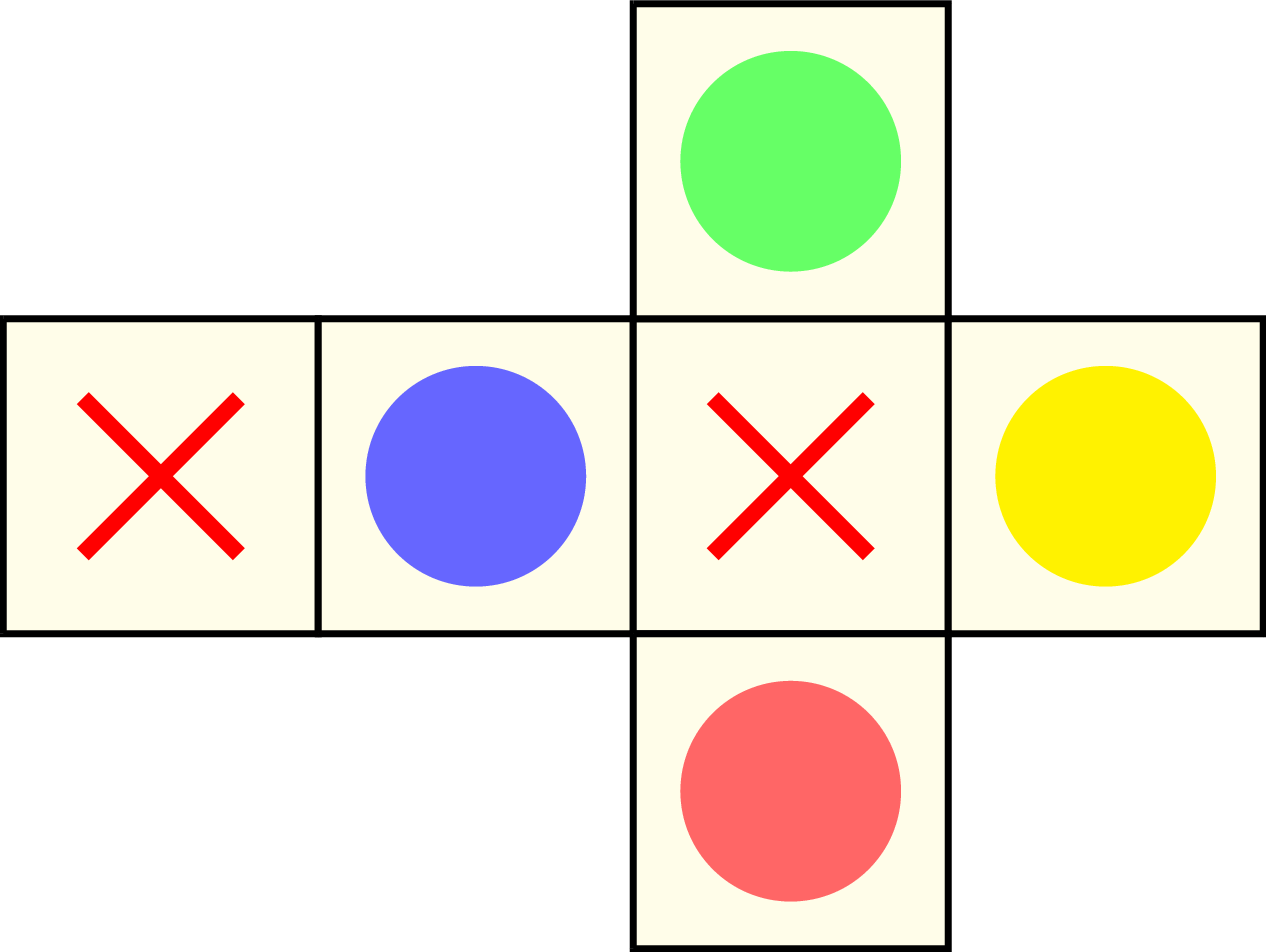
Le dé dispose ainsi de :
- deux faces Croix
- une face Bleu1
- une face Jaune
- une face Rouge
- une face Vert
Si on tire une face Croix, on passe son tour2. Si on tire une face colorée, le pion doit se rendre à la première case de cette couleur située devant lui. Nous pouvons donc avancer au maximum de 4 cases, dans le cas où nous tirons la couleur sur laquelle le pion est actuellement placé.
Le tableau ci-dessous résume de combien de cases nous avançons, d’une part selon la case où nous nous trouvons (axe horizontal du tableau) et d’autre part selon la couleur donnée par le dé (axe vertical du tableau).
| Je tire la face \ Je suis sur la case | Bleu | Jaune | Rouge | Vert |
|---|---|---|---|---|
| Bleu | 4 | 3 | 2 | 1 |
| Jaune | 3 | 4 | 1 | 2 |
| Rouge | 2 | 3 | 4 | 1 |
| Vert | 1 | 2 | 3 | 4 |
Dans le cas d’un dé parfaitement équilibré, on se rend bien compte que la mécanique de jeu est complétement équivalente à un jeu de l’oie classique où on remplacerait, dans le dé à six faces numérotées, les 5 et 6 par des Croix.
Oui mais, cela est-il toujours vrai dans le cas où on joue avec un dé pipé ?
Cas d’un dé pipé
Pour simplifier l’étude d’un dé pipé, je suis parti sur un jeu de l’oie particulier où les cases sont soit noires soit blanches. Nous remplaçons notre dé par une pièce présentant une face blanche et une face noire. La mécanique est similaire à notre jeu de période 4. Plus précisément, le tableau devient :
| Je tire la face \ Je suis sur la case | Blanc | Noir |
|---|---|---|
| Blanc | 2 | 1 |
| Noir | 1 | 2 |
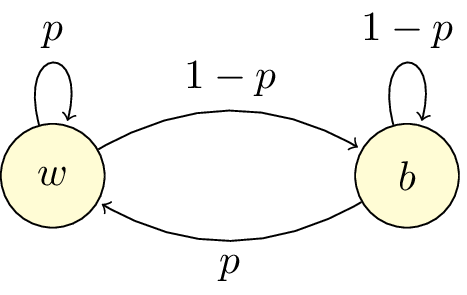
Notons $p$ la probabilité que la pièce tombe sur Blanc. La pièce est truquée si $p \neq 1/2$.
On peut représenter les probabilités de transition par le petit diagramme simplifié ci-dessous (w pour white, c’est-à-dire blanc; b pour black, c’est-à-dire noir).
Analyse des probabilités
Si on note $p_1$ (respectivement $p_2$) la probabilité d’avancer d’une case (respectivement de deux cases), alors nous pouvons montrer assez facilement, d’une part que :
\[p_1 = 2 p \cdot (1-p)\]et d’autre part que :
\[p_2 = 1 - p_1 = p^2+(1-p)^2\]Si nous traçons $p_1$ en fonction de $p$, nous obtenons la figure ci-dessous.
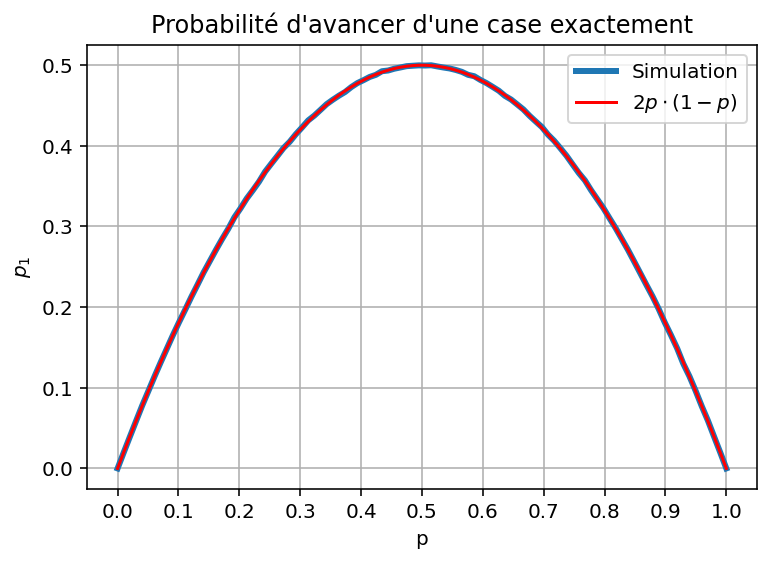
La courbe rouge correspond à notre modèle et la courbe bleue correspond à une simulation informatique sur un million de tirage. L’adéquation est parfaite.
Analysons un petit peu ces résultats.
Si $p=0$, alors la pièce tombera toujours sur Noir. Dès le premier coup, le joueur tombera donc nécessairement sur une case Noir. Après cela, toute nouvelle face Noir fera avancer systèmatiquement de DEUX cases. Nous aurons donc $p_1=0$ et $p_2=1$.
De la même façon, si $p=1$ alors la pièce tombera toujours sur Blanc. Juste après le premier coup nous serons donc sur une case blanche et nous avancerons alors systématiquement de DEUX cases. Nous avons donc de même $p_1=0$ et $p_2=1$.
Si $p=0.5$, nous sommes dans le cas d’une pièce parfaitement équilibrée. Dans ce cas là, Blanc et Noir sont interchangeables et nous avons autant de chances d’avancer d’une case que d’avancer de deux cases. Nous avons donc $p_1 = p_2 = 0.5$.
Nous remarquons ensuite deux choses :
- nous avons toujours $p_1 \leq 0.5$
- la courbe de $p_1$ est symétrique par rapport à l’axe $p=0.5$
Du premier constat, nous en déduisons qu’un joueur avançant plus fréquemment d’une case plutôt que de deux est plus susceptible d’utiliser une pièce truquée numérotée plutôt qu’une pièce truquée colorée.
Du second constat, nous apprenons que truquer la pièce en favorisant un côté donnera le même résultat quel que soit le côté favorisé.
On pourrait généraliser cela en utilisant notre dé à six faces et en le truquant mais… la flemme.
Par ailleurs et d’une façon complétement indépendante, les tarifications de mon hébergeur Gandi étant devenues scandaleuses, je pense ne pas renouveler mon abonnement et migrer ce blog sur une autre adresse. Du coup, cet article ne sortira probablement pas à la date à laquelle il a été écrit. C’est facheux mais c’est comme ça.